Introduction
In mathematics, functions is a common word we use everyday in class. Functions are very important in life as we encounter them everyday. Without functions, there will be no such things as algorithms in physics that will eventually lead to inventions and technologies of the future. A better understanding of functions can also be expressed in graphs to show what they look like.
transformations in functions
3 types:
translation
- Vertical Translation
f(x)+c will cause the function to shift upwards. (by ‘c’ units)
f(x)-c will cause the function to shift downwards. (by ‘c’ units)
- Horizontal Translation
f(x-c) will cause the function to shift to the right. (by ‘c’ units)
f(x+c) will cause the function to shift to the left. (by ‘c’ units)
Reflection
To graph y=-f(x), reflect the graph y=f(x) in the x-axis.
To graph y=f(-x), reflect the graph y=f(x) in the y-axis.
Shrinking & Stretching
- Vertical Shrinking and Stretching
When y=c f(x),
If c>1, the graph will stretch vertically. (by ‘c’ units)
If 0<c<1, the graph will shrink vertically. (by ‘c’ units)
- Horizontal Shrinking and Stretching
When y= f(cx),
If c>1, shrink the graph horizontally by a factor of 1/c.
If 0<c<1, stretch the graph horizontally by a factor of 1/c.
bike introduction
From the translation that I have learned in class, an assignment was given to us given below. We were told to use translations in functions to make a better model of a bike seen below.
While using Geogebra, I found out that the model of the bike between the given and Figure 1 appears to be different as seen below. Therefore, more adjustments in its function must be made to improve the model of the bicycle.
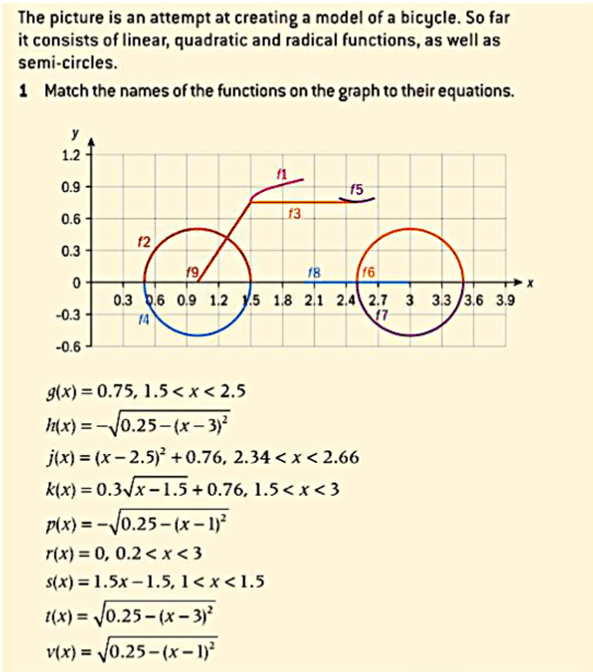
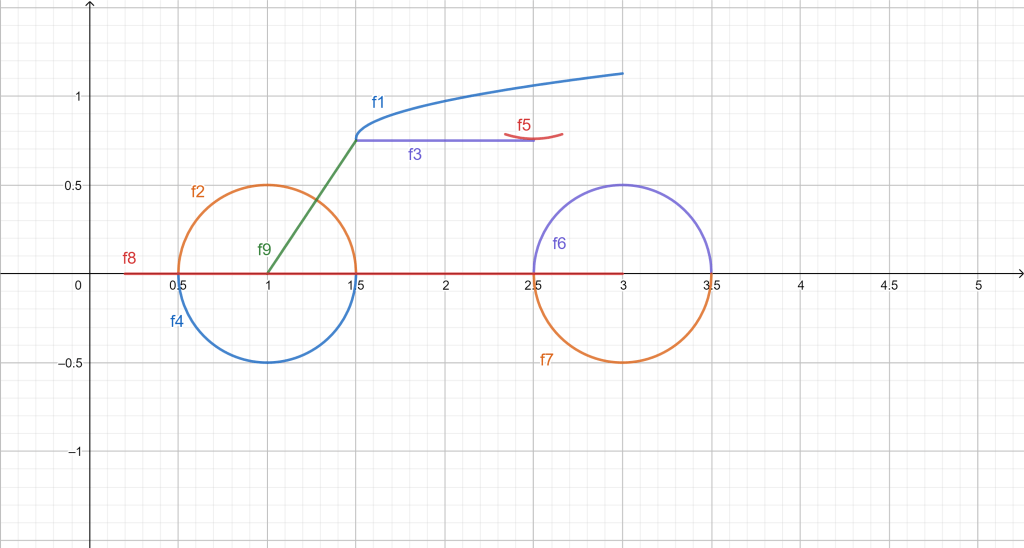
www.geogebra.org/graphing (First Model)
FIGURE 1: MULTIPLE FUNCTIONS GRAPHED TO LOOK LIKE A BIKE
k(x)=0.3*sqrt(x-1.5)+0.76, 1.5<x<3 = f1
v(x)= sqrt(0.25- (x-1)^(2)) = f2
g(x)=0.75, 1.5<x<2.5 = f3
p(x)= -sqrt(0.25- (x-1)^(2)) =f4
j(x)= (x-2.5)^(2)+0.76, 2.34<x<2.66 = f5
t(x)= sqrt(0.25- (x-3)^(2)) = f6
h(x)=-sqrt(0.25- (x-3)^(2)) = f7
r(x)=0, 0.2<x<3 = f8
s(x)=1.5x-1.5, 1<x<1.5 = f9
Due to the Inaccuracy of the bike’s first model, i’ve decided to remodel it by changing some functions and also by adding some more!
By changing :
- f1 into k(x)=0.3*sqrt(x-1.5)+0.76, 1.5<x<1.9
- f8 into r(x)=0, 1<x<2
By adding :
- f10 which is equal to y=-1.5x+4.5, 2.5<x<3
- f11 which is equal to y=1.5x-3, 2<x<2.5
- f12 which is equal to y=0.4, 2.266667<x<2.733333
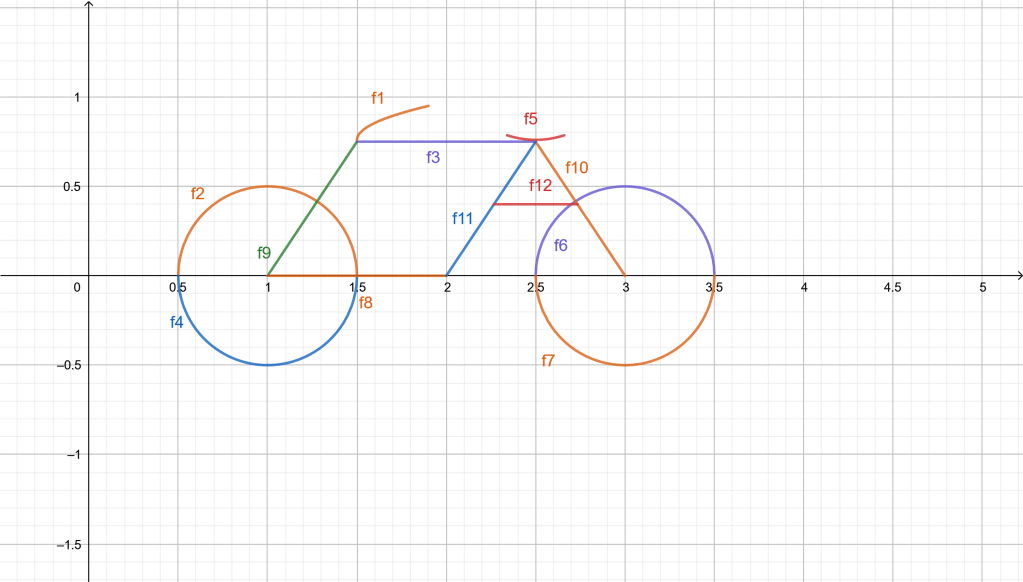
https://www.geogebra.org/graphing (Second Model)
figure 2: From the new model of the bike created, we can use it to travel around the world! This time, the bike will not break into pieces, not like the first model…
IB Learner profiles
thinkers
We use critical and creative thinking skills to analyse and take responsible action on complex problems. These thinking skills are used to be able to solve and graph different type of functions to be able to make a better model of bike.
Knowledgeable
We develop and use conceptual understanding, exploring knowledge across a range of disciplines. To be able to apply critical thinking, we need to understand the graph beforehand and how it works before improving the first model.
inquirers
We nurture our curiosity, developing skills for inquiry and research. Our curiosity enable us to begin with the thought of mind if graphing functions to look like a bike will be possible or not. This characteristics should be applied alongside a good knowledge and understanding, before critical thinking can be applied.
Wow, what a very informative post! As we’re learning about translations and transformations right now in Sec 4, I’ve just known that we could create translations and sizing effects using functions. This is very useful additional information, to what we’re learning right now, although pretty advanced for me, it is still very helpful for the future! Thanks!
LikeLike
Also, very fascinating way of using mere functions and formulas, to modify the shapes and lines, then creating a final result, of a bicycle.
LikeLike